Research
Publications:
- Karl Frinkle and Mike Morris
“Enabling Research into an Open Problem in Abstract Algebra through Undergraduate HPC Courses.”
Journal of Computing Sciences in Colleges, Volume 33, Issue 4, 2018, Pages 76-83
https://dl.acm.org/citation.cfm?id=3199583 - H. Neeman, K. Adams, J. Alexander, D. Brunson, S. P. Calhoun, J. Deaton, F. Fondjo Fotou, K. Frinkle, Z. Gray, E. Lemley, G. Louthan, G. Monaco, M. Morris, J. Snow and B. Zimmerman
“On Fostering a Culture of Research Cyberinfrastructure Grant Proposals within a Community of Service Providers in an EPSCoR State.”
Proceedings of the 2015 Annual Conference on Extreme Science and Engineering Discovery Environment (XSEDE ’15). ACM, (2015), Article 19, 8 pages.
http://dx.doi.org/10.1145/2792745.2792764 - Karl Frinkle and Mike Morris
“Developing a Hands-On Course Around Building and Testing High Performance Computing Clusters.”
Procedia Computer Science, Volume 51, 2015, Pages 1907-1916 (ICCS 2015)
ICCS 2015 International Conference On Computational Science
http://dx.doi.org/10.1016/j.procs.2015.05.455 - Mike Morris and Karl Frinkle
“A Three-Semester, Interdisciplinary Approach to Parallel Programming in a Liberal Arts University Setting.”
Proceedings of the 2014 Annual Conference on Extreme Science and Engineering Discovery Environment (XSEDE ’14). ACM, (2014), Article 66 , 7 pages.
http://doi.acm.org/10.1145/2616498.2616567 - K. Shiskowski and K. H. Frinkle
Principles of Linear Algebra With Mathematica
John Wiley & Sons, Inc., (2011) - K. Shiskowski and K. H. Frinkle
Principles of Linear Algebra With Maple
John Wiley & Sons, Inc., (2010) - K. H. Frinkle
“A Galerkin projection and multiple scales approach to Feshbach resonance in Bose-Einstein condensates.”
Mathematics and Computers in Simulation 74 (2007) 126–134.
http://doi:10.1016/j.matcom.2006.10.015
My Research Interest Include:
- Bose-Einstein Condensates
- Galerkin Approximations to Partial Differential Equations
- Dynamical Systems and Differential Equations
- High Performance Computing and Parallel Programming
Bose-Einstein Condensates
In the early 1920’s, Satyendra Nath Bose and Albert Einstein theorized that at extremely low temperatures, a new and exciting form of matter could be created for certain types of particles known as bosons. Bosonic particles, which include the photon, are allowed to share quantum states with each other. If one boson is in a particular quantum state, all nearby bosons are allowed to share the same quantum state. The more bosons that occupy the same quantum state, the stronger the tendency becomes for others bosons to join the same state. In such a state, a very large number of particle will have a single quantum wave function. Thus, if a tightly packed group of bosons is reduced to the lowest accessible quantum state, they would overlap, and it would not be possible to discern one atom from another. This would result in the creation of a super atom, or Bose-Einstein condensate (BEC). The first condensate was produced by Cornell and Wieman at JILA on June 5, 1995, using rubidium atoms cooled to one twenty-billionth of a Kelvin. Shortly after, other labs also started up production of condensates using various types of atoms in many different settings. Several interesting properties have already been observed in experiments, and more will surely come to light. One of the most promising properties seen so far is a condensates ability to slow down light. This is due to the fact that Bose-Einstein condensates can be made to have an extremely high gradient in the optical densities. Some experimentalists have used condensates to slow light down to a speed of only 17 meters per second. As a result, it has been theorized that condensates could be used to freeze a light pulse, and release it upon its demise.
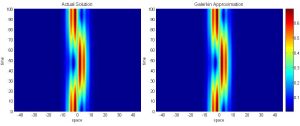
Of special iterest to me is the case of Feshbach resonance, which occurs when experimentalists periodically alternate the atomic interaction of the atoms in the condensate. This introduces very complicated dynamics to the governing model, the nonlinear Schrödinger Equation. It is my goal to understand fully the dynamics of this system. The main techniques that I employ are Galërkin projections and multiple scales.
In the above images, the spatial dimension is in the x-direction, and it evolves with respect to time in the y-direction. The norm squared of the solution is plotted with the corresponding scale located to the right. You can download a movie showing the temporal evolution of the initial condition along with the approximation *here*.
Pulse Localization and Dynamics in Fiber Grating Arrays
Recent excitement has been generated by the demonstration of photonic crystal fibers. It has been theorized that photonic crystal fibers can be thought of as fiber or wave guide arrays, the difference being the physical scale on which these two models are based. One then hopes that by understanding the behavior and properties of fiber arrays, then this might be of some importance in understanding the dynamics of pulse propagation in photonic crystal fibers. Photons travel much faster than electrons, and if incorporated into today’s technology, we would see an increase in the speed of information processing. However, similar to Bose-Einstein condensation, it may be some time before photonic crystals can be implemented practically. The main model for a fiber grating array is a system of Coupled-Mode Equations. I have been studying a 7-fiber linear array in which each fiber interacts with its nearest neighbor except for the outside 2, which interact only with the fiber to its interior. A similar model can be used for a fiber array which forms a cylinder, in which case all fibers interact with 2 others.
The following two images depict the backward (left) and forward (right) data of the middle fiber of a 7 fiber array. A gap soliton was used as an initial condition in the middle fiber only and with interaction betwen fibers turned on. As you can see, the data disappears from this fiber, and by clicking on the images, you can view the complete 7 fiber data plots.
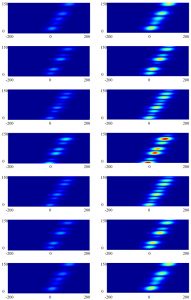 In the above images, the spatial dimension is in the x-direction, and it evolves with respect to time in the y-direction. The norm squared of the solution is plotted with dark blue corresponding to values close to zero. You can view an movie of the forward data as it evolves in time *here*, and one of the backward data *here*.
In the above images, the spatial dimension is in the x-direction, and it evolves with respect to time in the y-direction. The norm squared of the solution is plotted with dark blue corresponding to values close to zero. You can view an movie of the forward data as it evolves in time *here*, and one of the backward data *here*.