Dr Moretti’s Mathematica Notebooks – Applications
Mathematica Notebooks for Miscellaneous Applications
Important Note: Prior to 2016 our homepages would not allow me to post Mathematica notebooks directly on our site, so the majority of the notebook links will open a new window or tab with a Google Drive page. I will likely repost and update the links for earlier posts this summer.
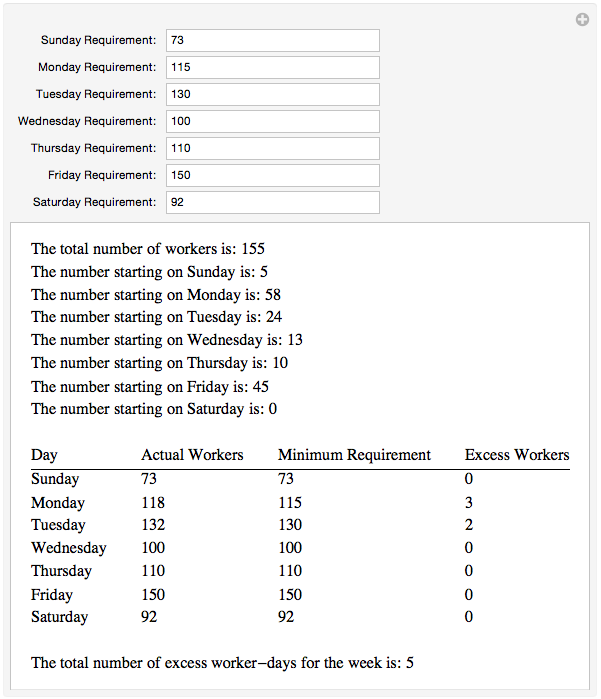
Work Scheduling
This notebook looks at a particular type of workforce scheduling where you know how many people are needed each day of the week and workers must work 5 days on followed by 2 days off. The problem is also generalized to include part-time workers with variable relative salaries and efficiencies.
Get a (non interactive) PDF of this notebook
Download this or any of my other Applications notebooks from Google Drive
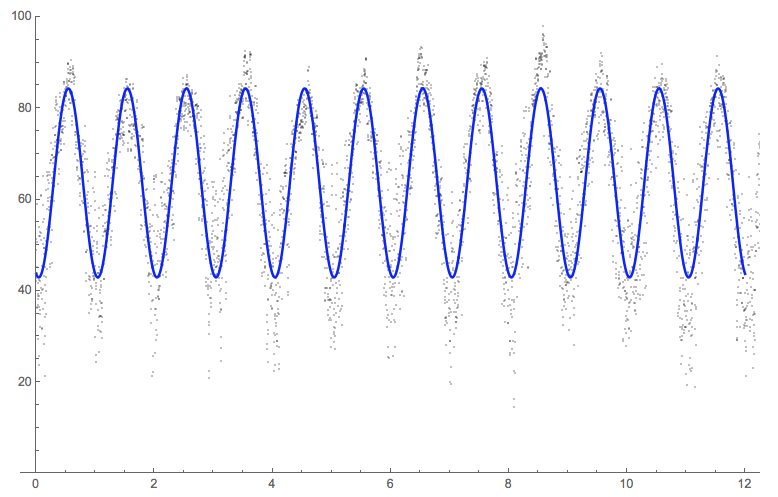
Modeling the Weather
This notebook shows an example of downloading weather information using Mathematica’s WeatherData command (in this case over a decade’s worth of daily average temperatures from the Durant area) and how to fit curves to it (both sinusoidal and triangular waves).
Get a (non interactive) PDF of this notebook
Download this or any of my other Applications notebooks from Google Drive
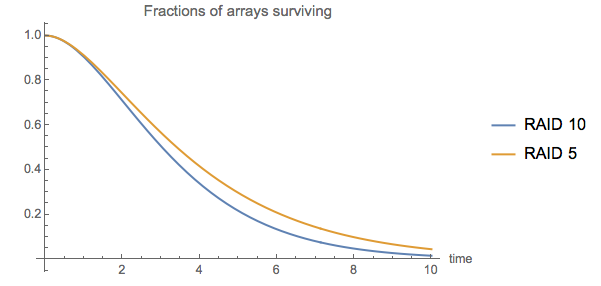
Reliability of Raid Arrays
This notebook looks at some basic reliability analysis (in this case for RAID 10 and RAID 5 arrays). Both types of hard drive arrays are discussed and Mathematica’s ReliabilityDistribution command is used to examine which type of array tends to last longer over time (given certain assumptions about the underlying hard drives).
Get a (non interactive) PDF of this notebook
Download this or any of my other Applications notebooks from Google Drive
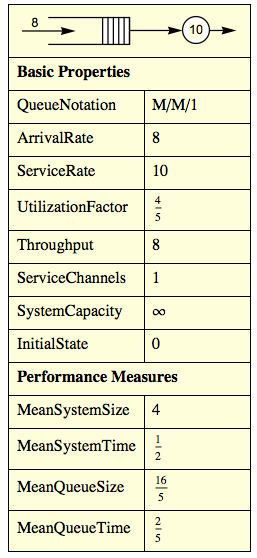
Queue Times
This notebook uses Mathematica’s QueueProcess command to look at the following question: If on average 8 people come in for help per hour, from the point of view of wait and service times is it better to have 1 representative who can help an average of 10 people per hour or 2 representatives who can help 5 people per hour? It also takes an example (based one in the Mathematica documentation) that looks at a network of queues (where people come to campus and look around, then get their parking permit, then get their course schedule).
Get a (non interactive) PDF of this notebook
Download this or any of my other Applications notebooks from Google Drive
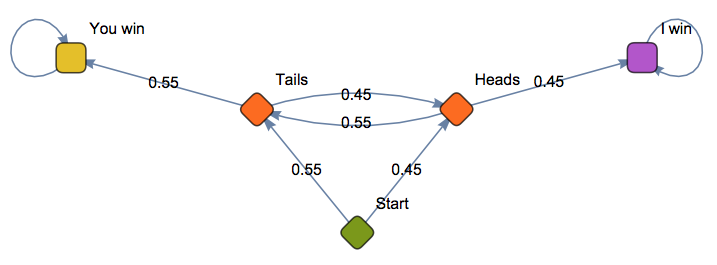
Modeling a Tennis Game as a Markov Chain
This notebook briefly defines a Markov chain (a tool in probability to model a system which can move between various states) and uses the example of a coin-flipping game to illustrate the basic ideas and how to set up a Markov chain in Mathematica. It then moves on to the much more complicated example of modeling a tennis game using a Markov chain with 4 parameters (the chance of faulting on the first and second serve and the chance of winning a point on the first and second serve) and uses it to look at questions about what kinds of practice are more effective.
Get a (non interactive) PDF of this notebook
Download this or any of my other Applications notebooks from Google Drive
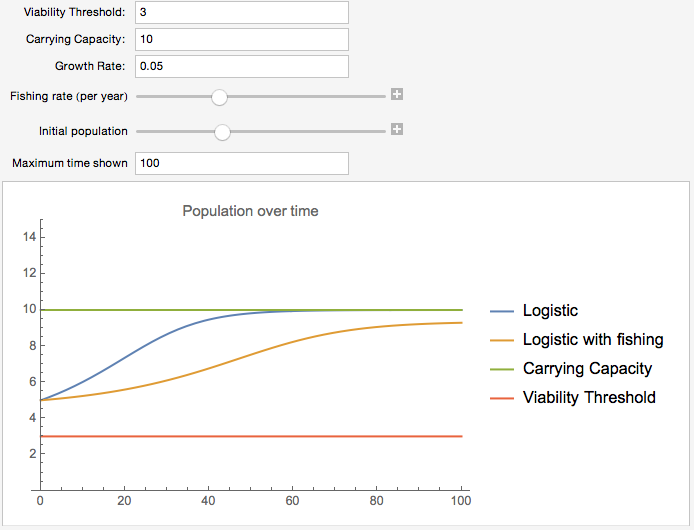
Population Models
This notebook looks at three common population models – the exponential growth model, logistic growth with a threshold, and logistic growth with a threshold together with hunting/fishing. Each model is briefly defined, and the logistic-type models have manipulations where you can look at the effect of various parameters like the growth rate, hunting/fishing rate, carrying capacity, etc.
Get a (non interactive) PDF of this notebook
Download this or any of my other Applications notebooks from Google Drive
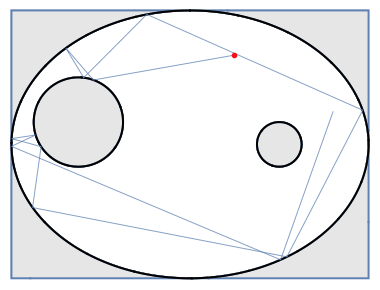
Billiard Paths
This notebook lets you look at the paths of a marble on arbitrarily shaped billiards table (such an elliptical table or a triangular table with a circular bumper in the middle). It also shows how this can be used to look at the reflective properties of the parabola and ellipse.
Get a (non interactive) PDF of this notebook
Download this or any of my other Applications notebooks from Google Drive
The Three-Way Duel Problem
In the Fall 2015 semester I gave a talk to the SE Math Club on the three-way duel problem (also known as the “Truel” problem). The Truel problem is where you have 3 shooters A, B, and C in a duel and they get to fire in that order. You don’t know the specific accuracy of the three shooters other than A is the worst (which is why A goes first) and C is the best (which is why C shoots last in the initial cycle). The question is how should A pick a target to maximize his or her chance of surviving the duel. I analyze the problem by modeling the Truel as a single Markov chain, where different strategies are represented via parameters in the chain. Mathematica is used both to find the results under different strategies and to see which of those results is the overall best. For my talk I didn’t assume anyone had worked with Markov chains before, so I include the same “coin-flipping” example as in the tennis application as an example.
Download a PDF of the Truel notebook
Download this or any of my other Applications notebooks from Google Drive
Demonstrating the Simplex Method
In the summer of 2016 I taught an Operations Research course. As part of relearning the material (which I had not taught in many years) I wrote some Mathematica commands to illustrate the Simplex method of solving linear programming problems (Mathematica has some great built-in commands of course, but they don’t show you the individual tableaus and pivoting process). The Simplex notebook contains commands for both maximization and minimization problems as well as examples of solving problems by both the 2 Phase and Big M methods. The code checks for unbounded and infeasible problem, and the pivoting switches to Bland’s method if the possibility of cycling is detected. There is also a command to perform some very basic sensitivity analysis for normal maximization problems.
Download the notebook from Google Drive