Dr. Moretti’s Mathematica notebooks – Differential Equations
Mathematica Notebooks for Differential Equations
Important Note: The links for the notebooks open a new window or tab with a Google Drive page – the current settings for our homepages won’t allow me to host mathematica notebooks locally.
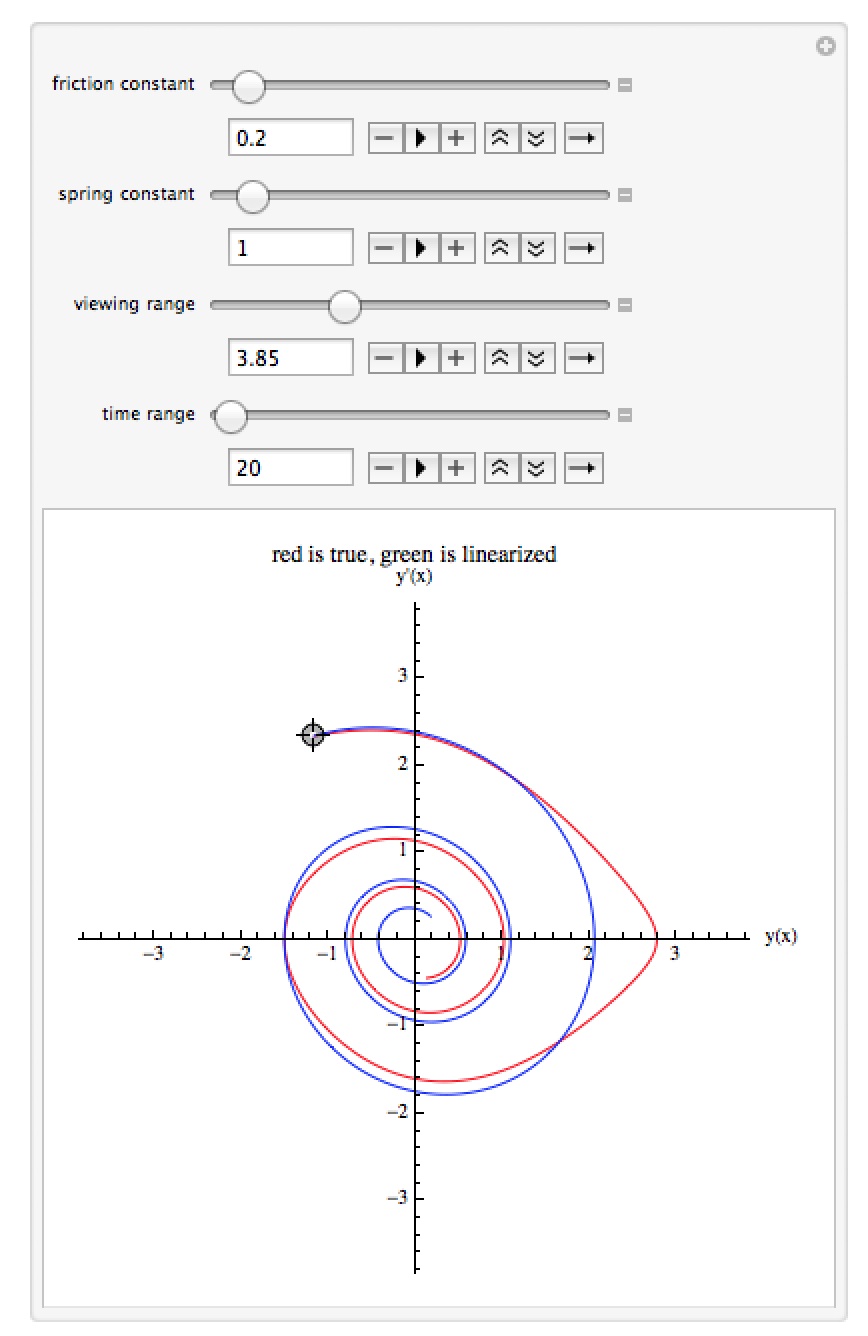
A Real and Linearized Pendulum
When simulating the motion of a pendulum the true equation is one which is not solvable exactly as it is nonlinear (for a unit mass it is y”+d y’+k sin(y)=0, where y is the angle of the pendulum, d is a friction constant, and k is a “spring constant” related to the length of the pendulum and gravity). When the angle y is small in size you can use linearization sin(y)~y to approximate the pendulum with the equation y”+d y’+k y=0, which is solvable exactly (this is why when talking about pendulums most high school physics textbooks have a small note in the margin along the lines “this is accurate is the angle of the swing is small, say less than 8°”). This notebook lets you see the graphs of the solutions to the real and linearized equations of the pendulum in the phase plane. You can move the starting point for both curves (linearized in blue/green, ideal in red) which corresponds to the initial values for the system – and as the initial angle/angular velocity gets larger, you can see the curves begin to separate (in fact if the initial angle is large enough the two curves can converge to different points!). The manipulation will let you change the values for the friction constant, spring constant, the viewing range for the graphs, and the time ranges of the solution curves.
Download this or other of my Differential Equations notebooks from Google Drive
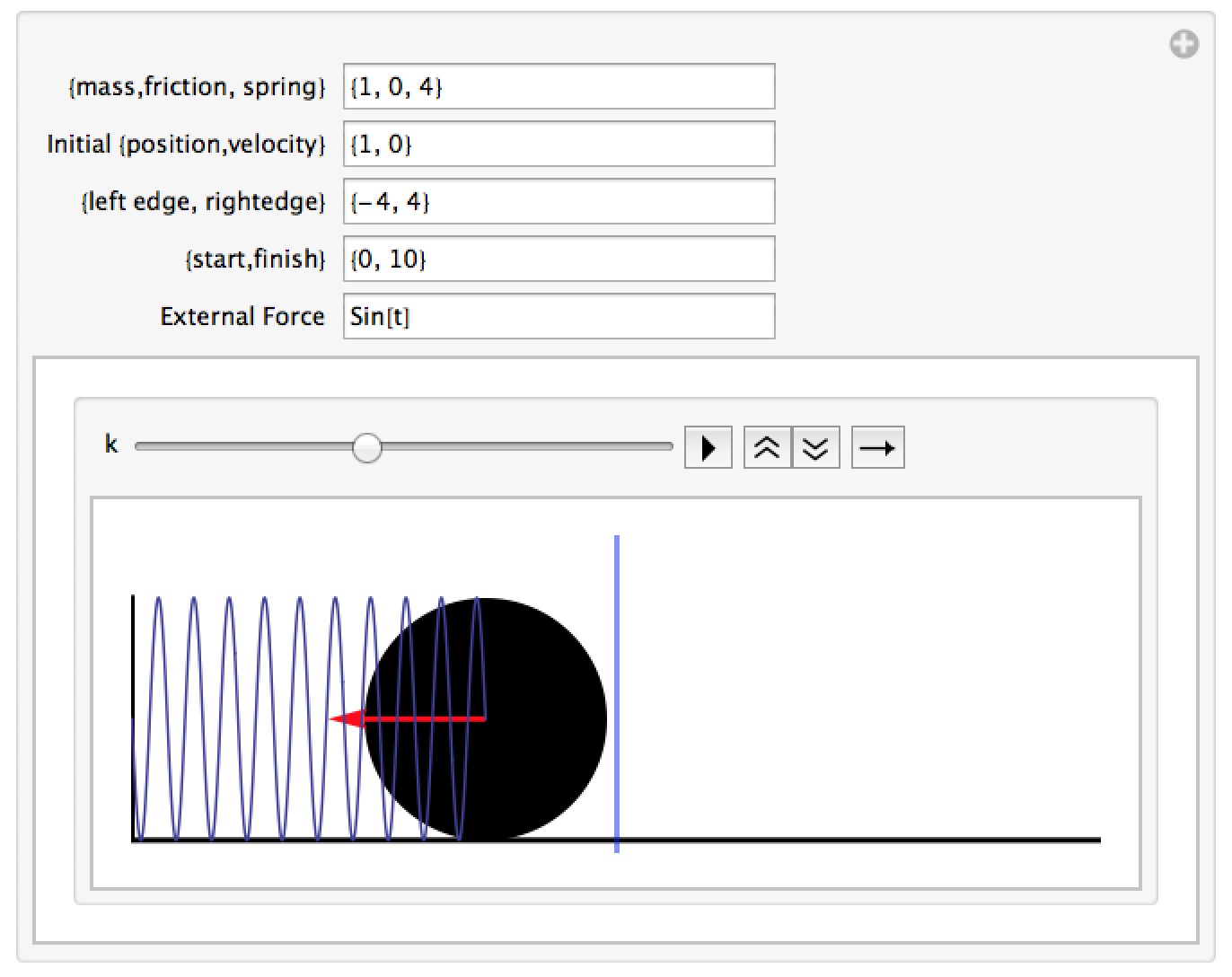
A Mass-Spring System
This notebook simulates the motion of a mass bouncing back and forth on a spring, possibly with an external force acting on it. You can change the mass, friction constant, spring constant, initial position and velocity, graphing range, time range, and external force (which is represented by a red arrow acting from the center of mass). You can use this to explore underdamping, critical damping, overdamping, and resonance.
Download this or other of my Differential Equations notebooks from Google Drive
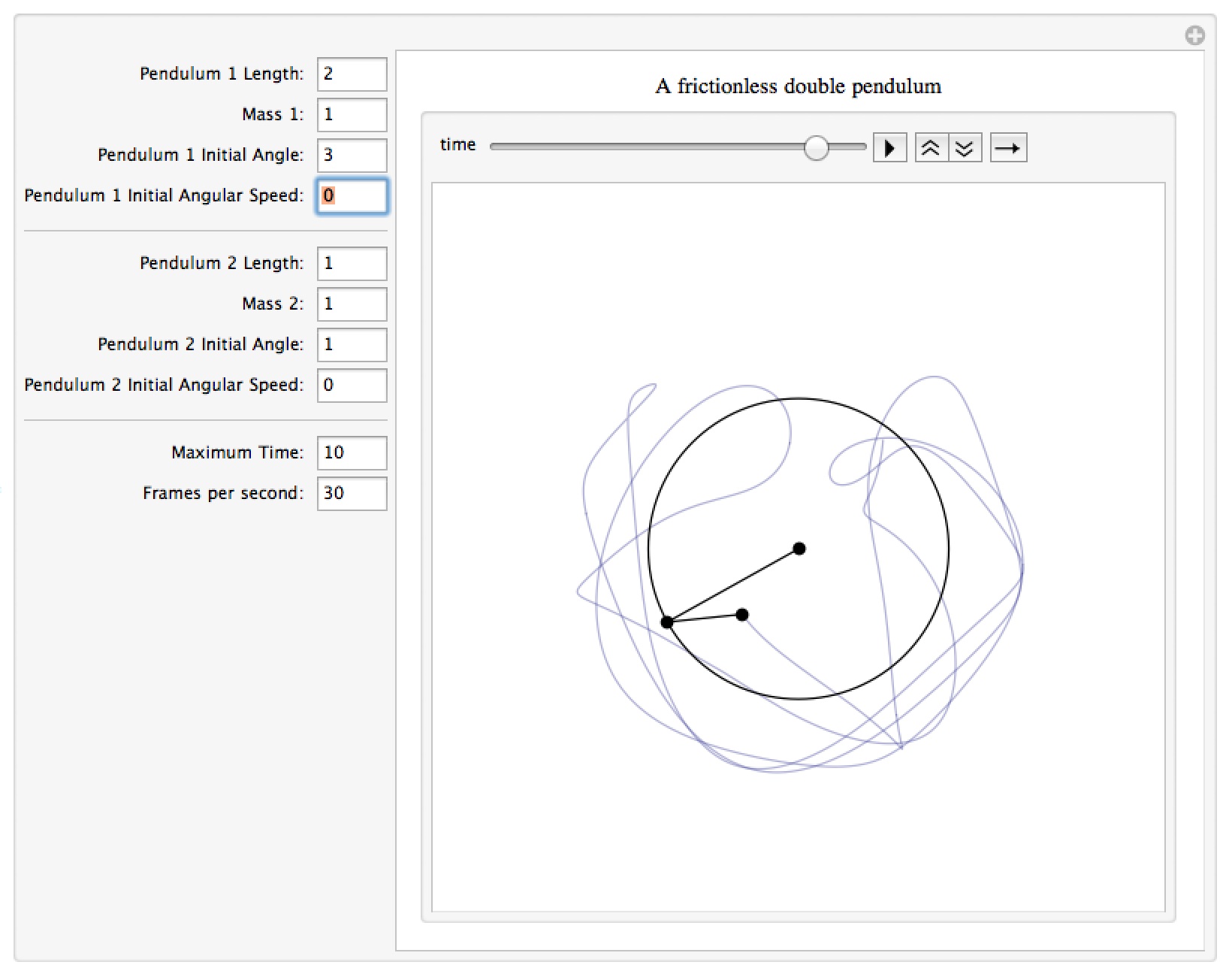
A Double Pendulum
This manipulation simulates an ideal double pendulum (i.e. frictionless with massless pendulum arms). You can change the pendulum lengths, bob masses, and initial angles and angular speeds. You can also control the time range and number of frames per second in the animation. Please note that I got the differential equations from the Double Pendulum page at Wolfram Research’s excellent Scienceworld site. Because of the animation this notebook is much larger than most of the ones I have posted.
Download this or other of my Differential Equations notebooks from Google Drive