Dr. Moretti’s Mathematica Notebooks – Calculus 2
Mathematica Notebooks for Calculus 2
Important Note: The links for the notebooks open a new window or tab with a Google Drive page – the current settings for our homepages won’t allow me to host mathematica notebooks locally.
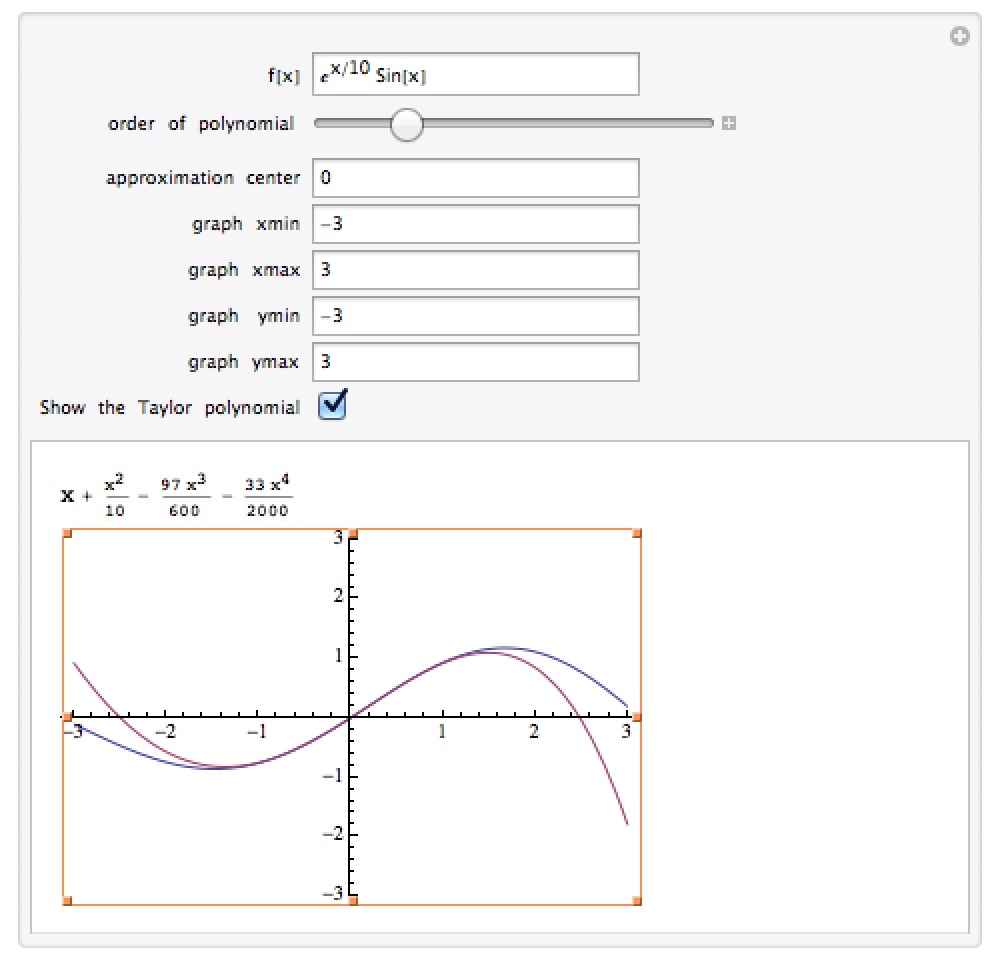
Taylor Polynomials
This notebook lets you look at the Taylor polynomials for a given function along with their graphs.
Download this or other of my Calculus 2 notebooks from Google Drive
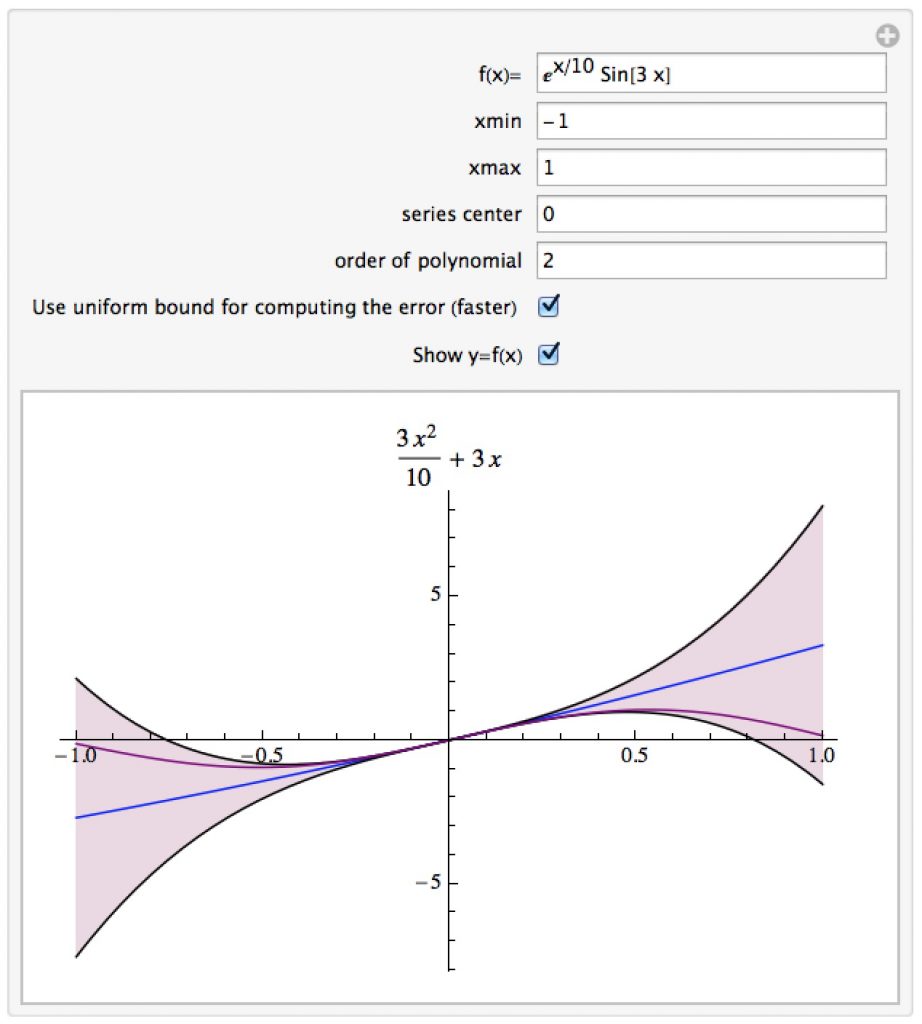
Errors in using Taylor Polynomials
Most Taylor polynomials are only approximations for their functions – at each point away from the center there is usually an error, and the size of the error is predicted by the Taylor Remainder Theorem. This notebook lets you graph and see a Taylor polynomial for a given function along with the error bounds predicted by the Remainder theorem. The graph of the original function f(x) appears in purple, the graph of the Taylor polynomial in blue, and the region in which the original function f(x) must be based on the error estimates is shaded in purple. The true graph of f(x) will always be in this region, but you can see that the farther away you get from the center of the approximation the wider this region gets (as the possible error gets larger). By default for speed purposes a uniform bound for the derivatives involved in the error is used; you can deselect that in the manipulation (which gets significantly slower but reduces the size of the error bounds and makes the band where the function must be smaller).
Download this or other of my Calculus 2 notebooks from Google Drive
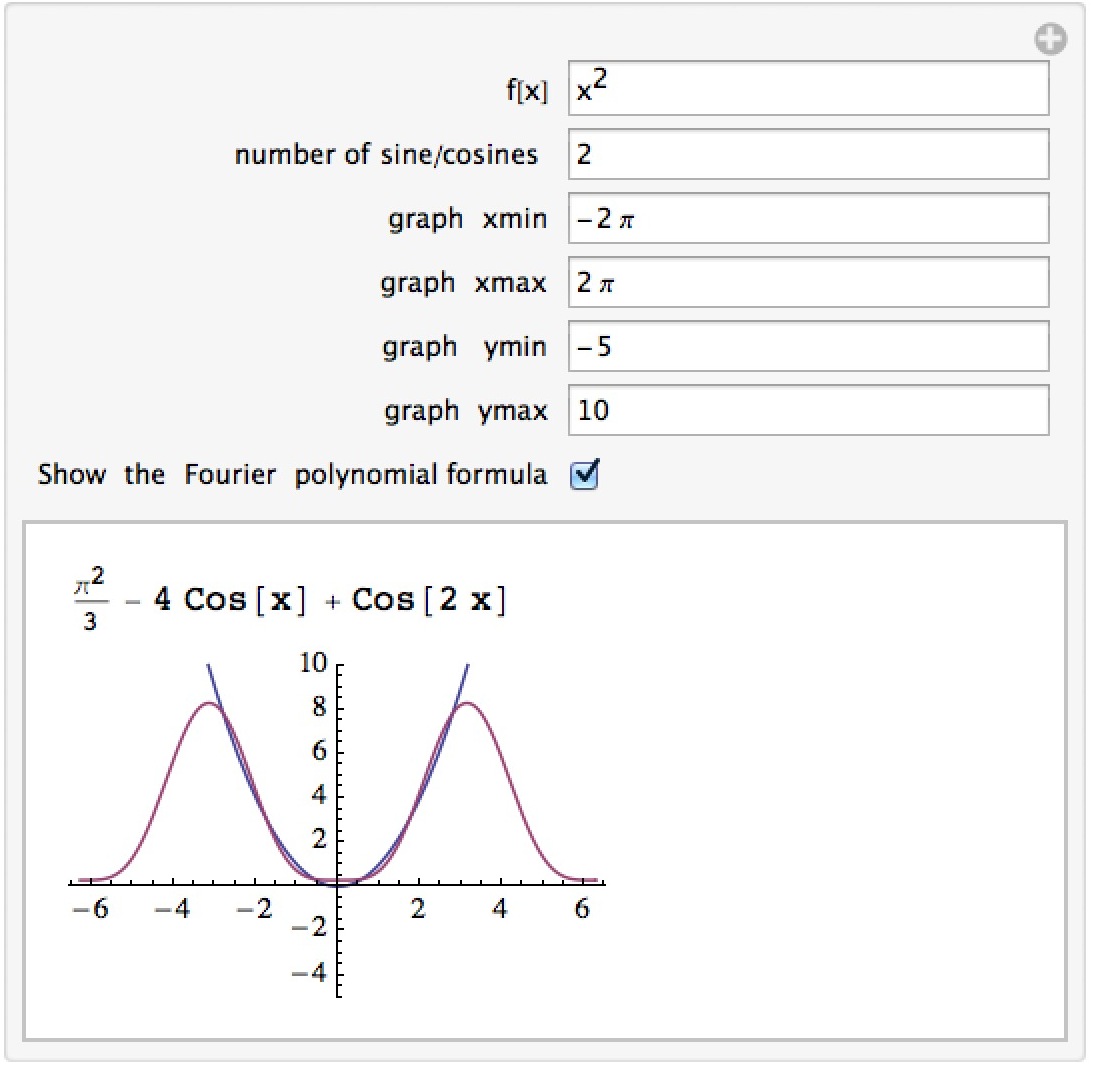
Fourier Polynomials
This manipulation lets you compute Fourier polynomials on [-π,π] for a given function and their graphs.
Download this or other of my Calculus 2 notebooks from Google Drive
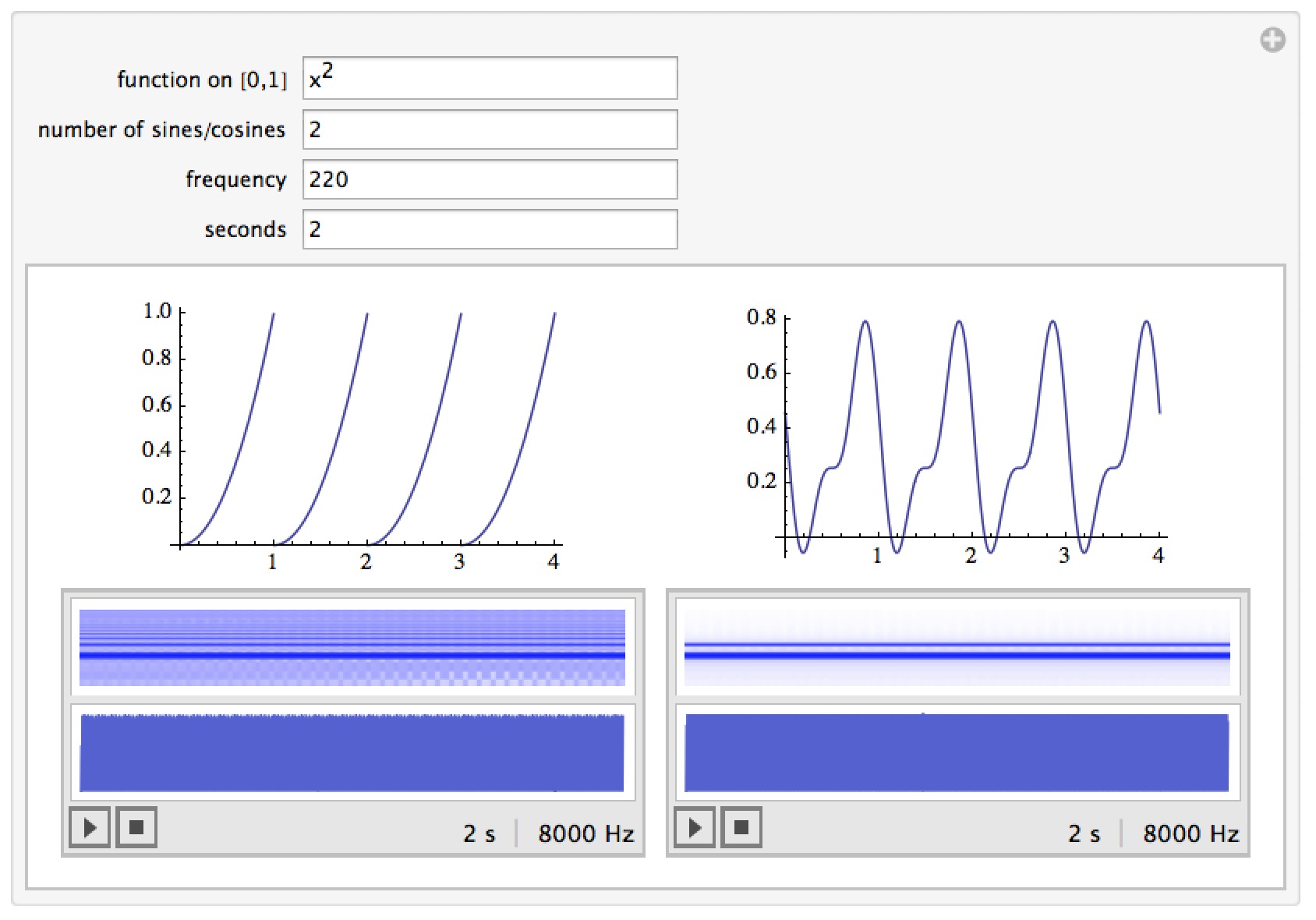
Fourier Polynomials and Sound
This notebook lets you explore the comparison to a function on [0,1] and its Fourier polynomial by converting them both into sounds you can play. As you take more terms in the polynomial you can both see the graphs converge and hear the sounds converge.
Download this or other of my Calculus 2 notebooks from Google Drive