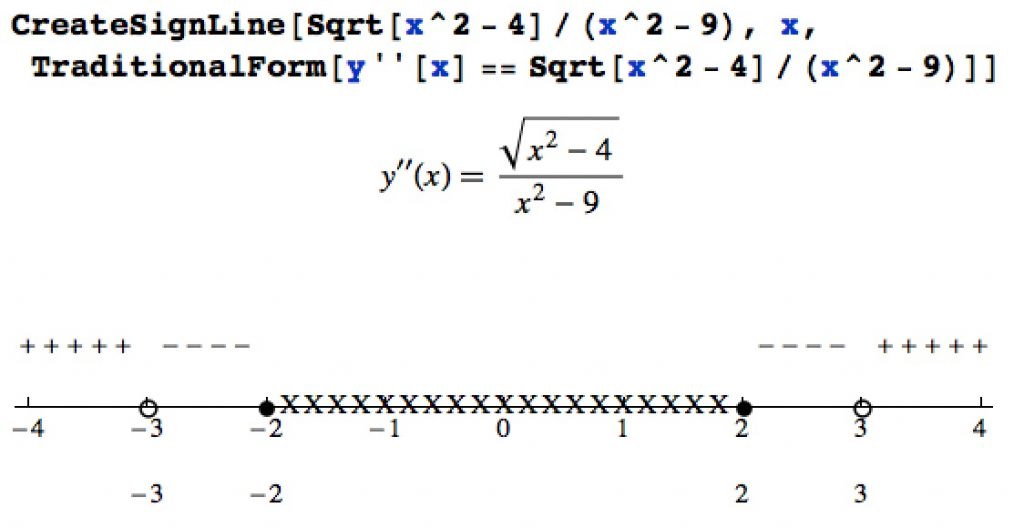Dr. Moretti’s Mathematica Notebooks – Calculus 1
Mathematica Notebooks for Calculus 1
Important Note: The links for the notebooks open a new window or tab with a Google Drive page – the current settings for our homepages won’t allow me to host mathematica notebooks locally.
Epsilon-Delta definition of Limits
This notebook has a manipulation which lets you explore the ε-δ definition of limits. For the limit to exist no matter how narrow you make the gap between the horizontal red lines, you should be able to force the blue-shaded portion of the curve to be between them if you make the vertical blue lines sufficiently close together.
Download this or other of my Calculus 1 notebooks from Google Drive
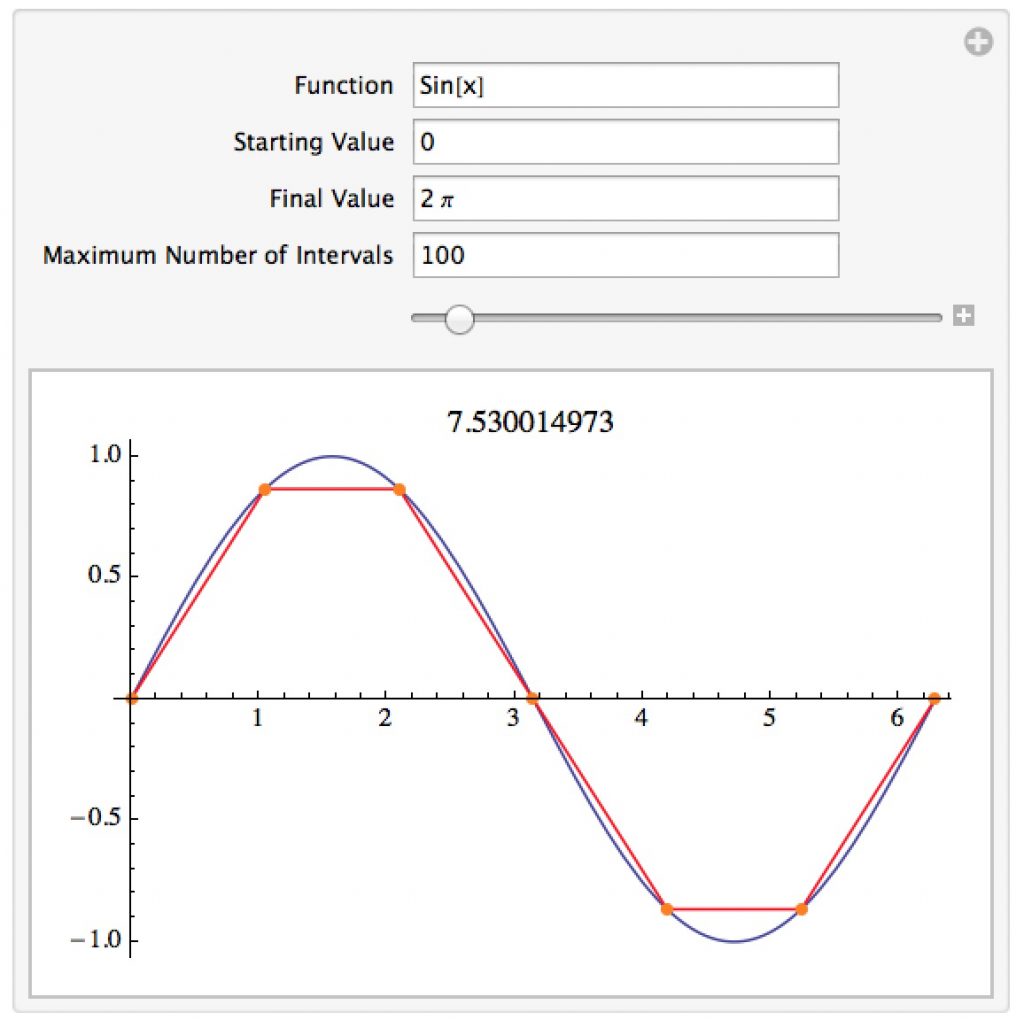
Estimating Arclength
This notebook lets you explore the definition and way to estimate arc length of a curve by adding the lengths of straight line segments.
Download this or other of my Calculus 1 notebooks from Google Drive
Estimating The Graph of the Derivative
This notebook lets you explore the notion of the derivative as a function. It lets you slide the tangent line along the graph of the original function and watch the graph of the derivative be constructed on the right.
Download this or other of my Calculus 1 notebooks from Google Drive
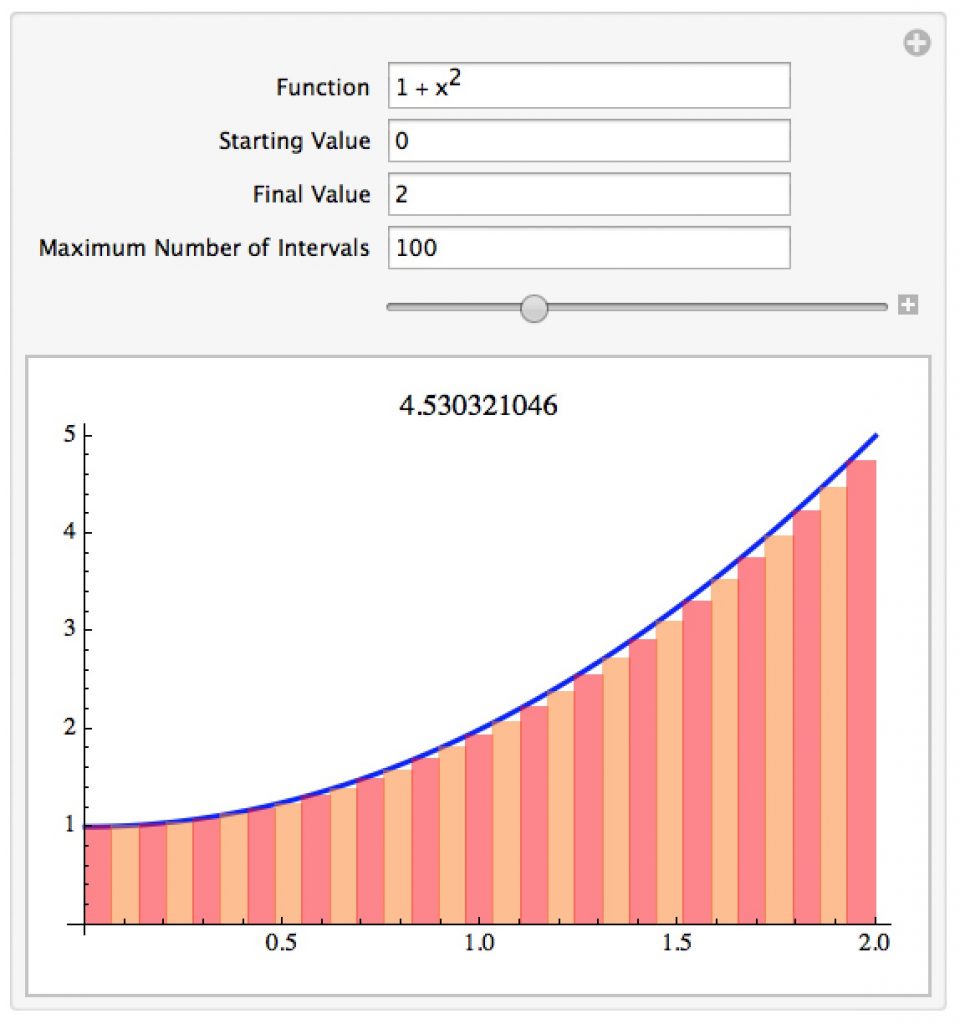
Estimating Signed Areas by Riemann Sums
This notebook lets you explore the notion that the area under the curve can be found by approximating the region with rectangles and letting that area estimate get better and better by using more and more rectangles.
Download this or other of my Calculus 1 notebooks from Google Drive
Volumes by Cross Sections
This notebook lets you explore the idea of finding volumes by cross-sections. You pick the curves that form the “base” of the solid as well as the type of cross-sections (triangular, circular, etc.). The manipulation then creates an approximation of the solid in 3D and computes the volume.
Download this or other of my Calculus 1 notebooks from Google Drive
Volumes of Revolution
This notebook lets you look at volumes of revolution – you can spin the region bounded by two curves around either the x-axis or y-axis.
Download this or other of my Calculus 1 notebooks from Google Drive
Area Functions
This notebook lets you graph an “area function” from calculus – that is, the graph of the signed area underneath a function y=f(x) from a starting point x=a. This is a key idea behind the Fundamental Theorem of Calculus. The areas under the graph of the original function are shaded with positive area being blue and negative area being red. In the picture below you can see the area function (on bottom) beginning to decrease as in the top graph we are picking up negative area.
Download this or other of my Calculus 1 notebooks from Google Drive
Moving a Couch Around a Corner
This notebook demonstrates the process of moving a couch around an “L” corner so you find the longest couch that can make it around. This couch is actually the shortest of the ones that get stuck. A version of this appears in the Wolfram Demonstrations Project, and I wrote an article for the College Mathematics Journal about how to find the longest couch in general.
Download this or other of my Calculus 1 notebooks from Google Drive
Sign Lines
Finding when a function is positive or negative is really an algebra problem, but it comes up in calculus (when the derivative is positive the original function is increasing, etc.). While not foolproof, this notebook provides commands to attempt to construct a “sign line” for a given function (with a label). It works best with algebra-oriented functions, and is very helpful when doing calculus-based graphing (in fact I wrote this to help write solutions to review sheets in Calculus 1). The X’s in the picture below indicate an interval on which the function isn’t defined.
Download this or other of my Calculus 1 notebooks from Google Drive
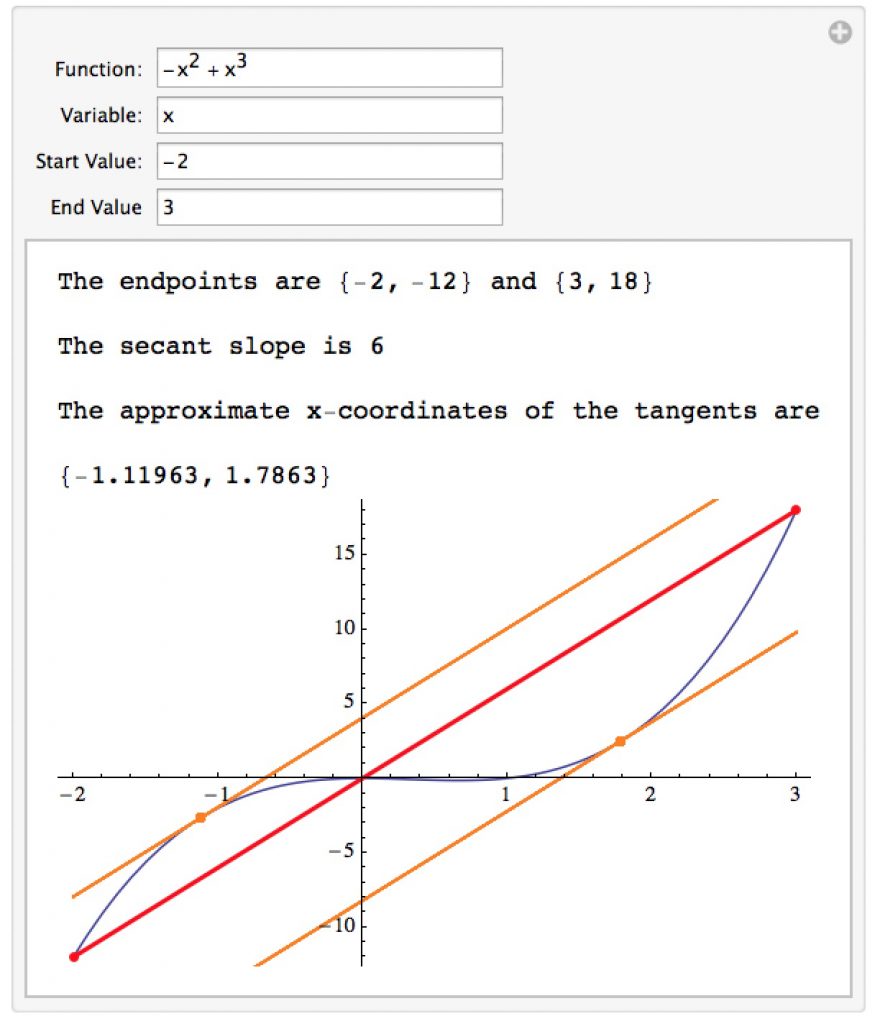
The Mean Value Theorem
This notebook illustrates the Mean Value Theorem from calculus, which essentially states that under the right conditions when you have a function f(x) on the closed interval [a,b], there will be at least 1 point x=c in the interval where the tangent line to the curve will be parallel to the line joining the ends of the graph.
Download this or other of my Calculus 1 notebooks from Google Drive